Unités de longueur : les grandes, les petites
- Détails
Dans certaines des pages web du département ARTEMIS, vous trouverez des nombres astronomiques ; sur d’autres, des quantités microscopiques... parfois les deux sur une même page. Pour vous aider, nous allons illustrer ces unités afin qu’elles soient un peu plus parlantes. Nanomètres ? Mégaparsecs ? Voici quelques repères pour vous guider parmi les unités de longueur, conventionnelles, ou spécifiques (astronomiques ou microscopiques).
La définition actuelle du mètre fait référence à la propagation de la lumière dans le vide : en 1 seconde, la lumière parcourt 299 792 458 mètres, exactement.
On peut noter que l’histoire du mètre et celle de la seconde sont depuis longtemps intimement liées. Déjà en 1675, la définition du mètre était la longueur du pendule dont la demi-période est d’une seconde.
Les schémas ci-dessous donnent un panorama des unités de longueur : en flèches noires, les unités conventionnelles, celles que nous devrions utiliser, et en rouge des unités pratiques, adaptées à certaines situations précises. En bleu des "repères" sont donnés, pour aider à se faire une idée des ordres de grandeur (...ou de petitesse !). Par exemple, 1 pétamètre (1015m, 1000 milliards de km), c’est 200 fois plus grand que l’orbite de pluton, mais c’est pourtant tout petit devant la distance à l’étoile la plus proche.
En allant vers les plus petites dimensions :
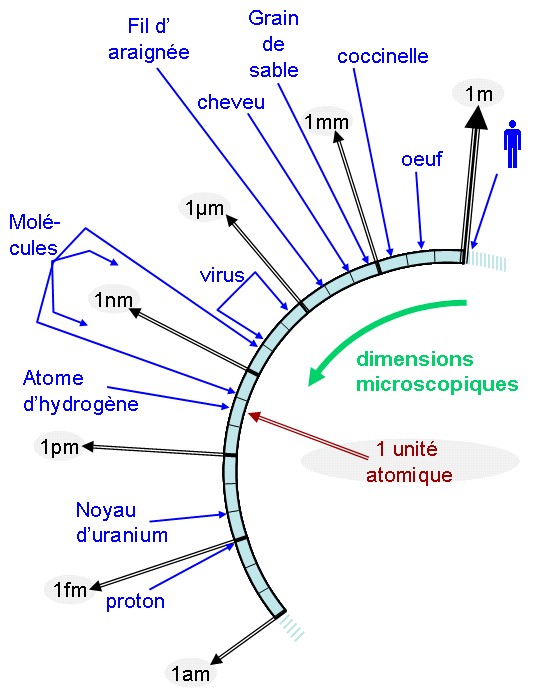
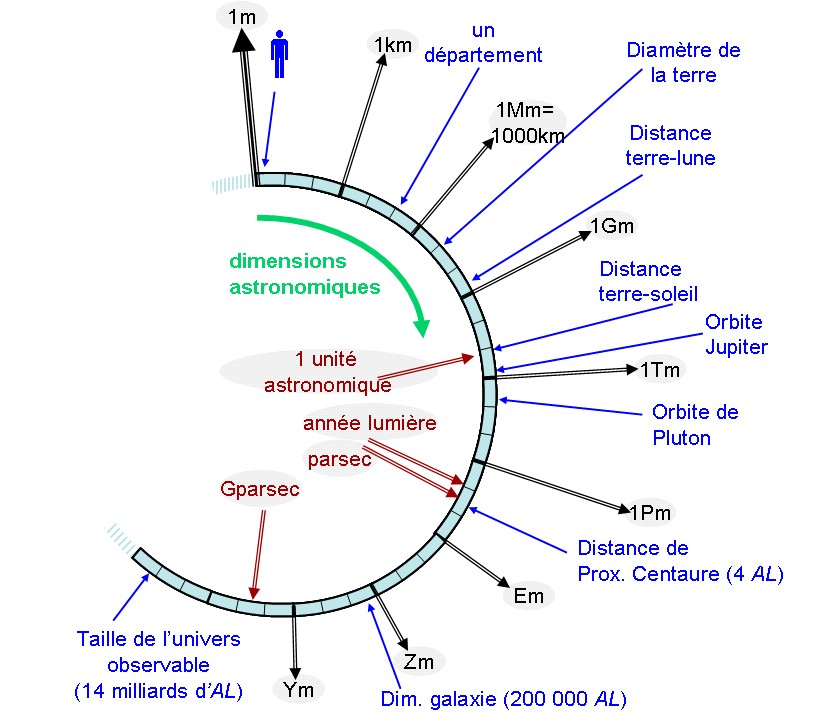
En allant vers les plus grandes dimensions :
Unités microscopiques :
Le millimètre mm (millième de mètre, 10-3m). Il est difficile de manipuler avec ses doigts un objet plus petit que 1mm.
Le micromètre ou micron µm (millième de mm, 10-6m) : l’épaisseur des bulles de savon, quand elles font de jolies couleurs, est de quelques microns.
Le nanomètre nm (millième de µm, 10-9m) : c’est la taille d’une petite molécule comme la molecule d’octane.
Le picomètre pm (millième de nm, 10-12m) : Une dizaine de pm c’est l’amplitude de vibration typique du tympan de l’oreille humaine pour un son à la limite d’audibilité (c’est beaucoup plus petit que la taille de l’atome d’hydrogène, pourtant le plus petit des atomes !).
Le femtomètre fm (millième de pm, 10-15m) : l’échelle de taille des noyaux atomiques. On dit aussi "1 fermi", du nom du physicien italien.
L’attomètre am (millième de fm, 10-18m) : Il n’y pas d’ "échelle naturelle" au niveau de l’attomètre. La matière n’a pas de structure avérée à cette échelle ou à des échelles plus petites, on ne considère plus que des particules élémentaires, (électrons, quarks, neutrinos...) sans structure et sans taille.
En allant vers les grandes longueurs :
Le kilomètre km (mille m, 103m) : à partir de quelques km on hésite à faire un trajet à pied...
Mille km (103 km ; on devrait écrire Mm, mais l’usage est de dire 1000 km plutôt que 1Mégamètre...) : C’est la dimension d’un pays comme la France. Le diamètre de la terre est d’environ 13 000 km.
Million de km (106 km ; on devrait écrire Gm, pour gigamètre) ; typiquement un aller-retour terre-lune.
Milliard de km (109 km ; on devrait écrire Tm, pour Téramètre) ; typiquement la distance soleil-jupiter, ou encore la distance que parcourt la terre en une année sur sa trajectoire autour du soleil.
En astronomie, des unités spécifiques ont été introduites, afin d’éviter de manipuler des nombres toujours plus grands.
L’unité astronomique (UA) est par définition la distance moyenne terre-soleil : 0,15 milliard de km ; utile pour exprimer les distances à l’intérieur du système solaire. Attention :"ua" (en minuscules !) désigne également l’unité atomique (le "rayon de Bohr" de l’atome d’hydrogène), qui donne l’échelle naturelle des distances pour les atomes, molécules, arrangements cristallins. L’unité atomique valant 53 picomètres, il y a peu de risques de confusion avec une unité astronomique, 3000 milliards de milliards de fois plus grande !
L’année-lumière : (AL) la distance que parcourt la lumière en une année. Par comparaison, 1UA vaut à peine 8 minutes-lumière...
Le parsec (pc) : par définition, c’est la distance d’où un observateur verrait la trajectoire de la terre autour du soleil comme ayant une demi-ouverture d’une seconde d’arc : 1pc vaut donc environ 200 000 UA. Ou encore 3,26 AL. La distance moyenne entre galaxies est typiquement d’un mégaparsec (1 Mpc).
Suivant les cas on préférera le parsec ou l’année-lumière, non pas parce que leur valeur est différente, mais parce qu’elle évoquent une situation physique différente (la propagation de la lumière dans un cas, la parallaxe de l’orbite de la terre dans l’autre), qui génèrent différentes échelles naturelles de distance. Une situation analogue se produit en physique atomique où coexistent deux unités, également voisines, l’Angström Å (100pm) et l’unité atomique (53pm).
L’erreur cyclique en instrumentation
- Détails
Pollution d’un signal périodique par un signal de même fréquence : l’Erreur cyclique. Même s’ils ne l’abordent pas de la même façon, les deux projets , T2M et liade, actuellement développés dans le cadre de l’activité télémétrie laser d’ARTEMIS, ont en commun de devoir faire face au problème des erreurs cycliques.
L’erreur cyclique affecte une mesure de phase chaque fois que la mesure d’un signal périodique est polluée par un autre signal de même fréquence. Le diagramme phase-amplitude (voir plus bas) est très pratique pour comprendre ce qui se passe :
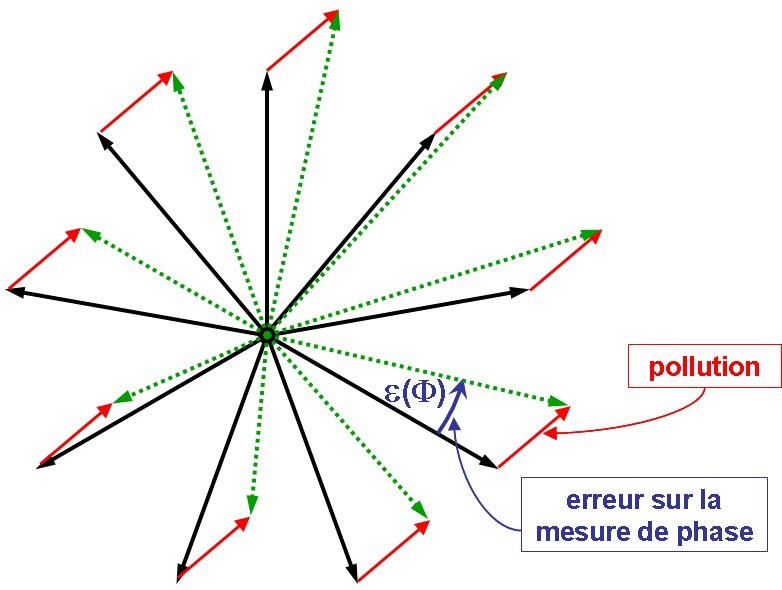
La phase du signal (vecteur) noir étant à mesurer, on voit que la mesure est affectée par la présence du signal rouge qui a pour effet de décaler la phase et entraîne une erreur de mesure. Cette erreur n’est pas facile à corriger, car elle est fonction de la phase et de l’amplitude de la pollution, mais aussi de la phase et de l’amplitude du signal. Cette variation est périodique, d’où le nom d’erreur cyclique.
La phase détectée est ainsi presque toujours fausse. Pour les valeurs de F où l’erreur de phase e(F) s’annule, c’est l’erreur sur l’amplitude qui est maximale.
Représentation phase-amplitude d’un signal
Cette représentation très pratique est utilisable chaque fois que vous considérez l’addition de deux signaux périodiques de même fréquence.
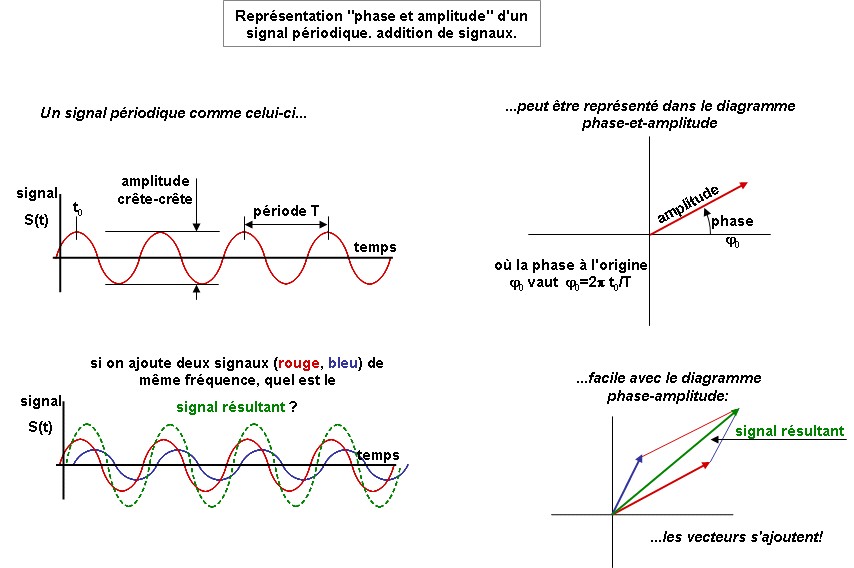
La généralisation au cas de deux signaux de fréquences différentes est naturelle : un des deux vecteurs tourne, avec une vitesse angulaire qui est la différence des pulsations des deux signaux. L’extrémité du vecteur résultant décrit donc au cours du temps (à la fréquence différence), un cercle dont le rayon est la différence des amplitudes des deux signaux.
Ces raisonnements sont toujours valables, quel que soit le phénomène oscillatoire en jeu : il s’applique aux cas où deux signaux électriques s’ajoutent, ou encore pour rendre compte de l’interférence de deux ondes optiques de même fréquence ou de fréquences voisines.
En mécanique aussi...
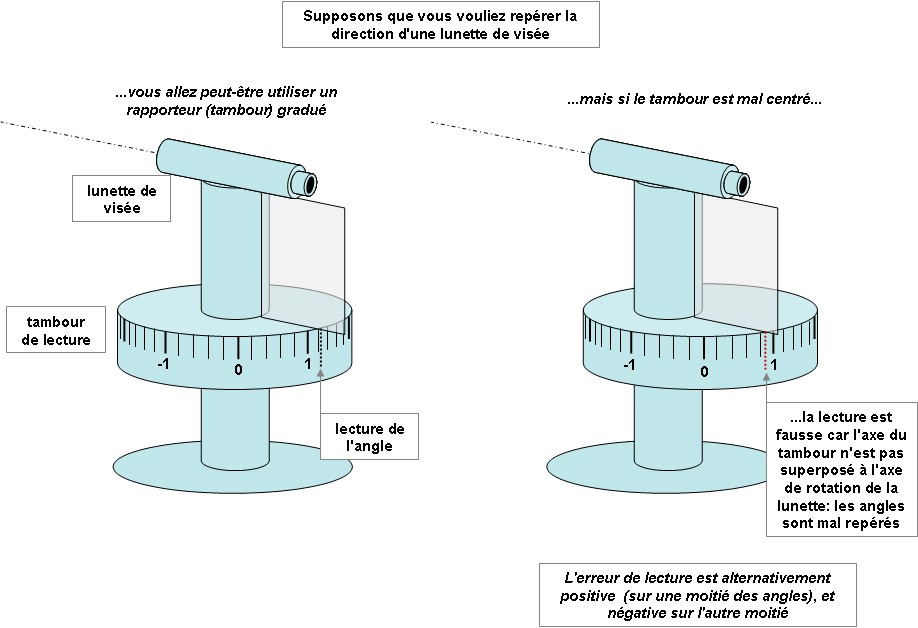
La mesure des angles et le rapporteur mal centré
L’erreur cyclique est très classique en instrumentation. Avant même l’électronique, elle était déjà présente dans la mesure des angles : lorsqu’on mesure des angles sur un rapporteur mal centré, la mesure la mesure est affectée de la même façon.
Quelques méthodes de Télémétrie Laser
- Détails
Télémétrie par temps de vol
Si on mesure le temps que met la lumière pour aller jusqu’à un réflecteur sur la cible et revenir, alors on connaît la distance de la cible, car la vitesse de la lumière dans le vide a une valeur, 299 792 458 m/s, parfaitement définie du fait du choix des unités de longueur et de temps.
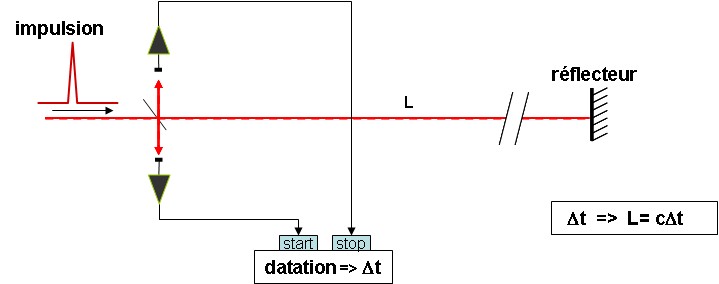
Cette télémétrie dite "de temps de vol" est utilisée depuis déjà plusieurs dizaines d’années. Elle permet de mesurer, avec une exactitude meilleure que le centimètre, la distance Terre-Lune, ou encore la distance de satellites en orbite basse.

Installations de télémétrie par temps de vol (Terre-satellite, Terre-Lune) du laboratoire GéoAzur, Observatoire de la Côte d’Azur.
Télémétrie par modulation de porteuse
Pour les résolutions nanométriques visées ici, nous développons des mesures de distance avec des faisceaux laser dont l’intensité est modulée à très haute cadence. L’effet physique utilisé (la propagation de la lumière à une vitesse finie et parfaitement connue) est le même que pour la télémétrie par temps de vol, mais la mesure peut être faite en permanence, sans attendre que le faisceau ait fait l’aller-retour : on peut donc en quelque sorte "accumuler" des données sans "perdre le temps" de l’aller-retour d’une impulsion lumineuse isolée.
La mesure ainsi obtenue n’est alors que la mesure de l’excédent fractionnaire du nombre de "longueurs d’onde synthétique" (la longueur d’onde synthétique s’écrit Lºc/F où F est la fréquence de la modulation et c la vitesse de la lumière). Si la mesure est réalisée à une fréquence F fixe, elle ne peut donner de résultat absolu (sauf pour les très petites distances, inférieures à L, ce qui n’est bien sûr pas notre objectif). Il faudra donc trouver ou reconstituer l’information manquante pour déterminer le nombre entier de longueurs d’onde synthétique.
Télémétrie par interférométrie homodyne
Elle repose sur l’interférence à deux ondes (comme, par exemple, dans l’interféromètre de Michelson ou plus. Comme dans le cas de la télémétrie par modulation, si le faisceau utilisé est un faisceau monochromatique de longueur d’onde fixe, on mesure un excédent fractionnaire. Comme la longueur d’onde optique est de l’ordre du micron, on atteint des résolutions nanométriques voire sub-nanométriques sur des déplacements. En revanche, il n’est a priori pas possible de réaliser une mesure absolue de distance par interférométrie sans faire varier la longueur d’onde du faisceau.
Les projets de télémétrie laser au sein d’ARTEMIS utilisent des faisceaux laser dont l’intensité est modulée.
- Le projet T2M a déjà permis d’obtenir un prototype de télémètre, en cours d’amélioration. Il repose sur la mesure de la fréquence de la modulation qui permet d’annuler la phase de propagation aller-retour jusqu’à la cible.
- Le projet Iliade est en cours de mise au point. Au contraire de T2M, il travaille à fréquence fixe : on mesure alors des phases dont on tire la distance. Iliade recourt à des mesures de temps de vol pour déterminer la distance absolue.
Même s’ils ne l’abordent pas de la même façon, les deux projets ont en commun de devoir faire face au problème des erreurs cycliques (voir le fichier correspondant), problème très classique en instrumentation.

Le montage du télémètre Iliade met en oeuvre simultanément une mesure d’interférence homodyne et une mesure de modulation.
Enfin signalons, bien qu’elle ne soit pas employée sur les projets T2M et Iliade d’ARTEMIS, la télémétrie hétérodyne :
La télémétrie hétérodyne utilise, comme la télémétrie homodyne, l’interférence entre deux faisceaux monomodes, mais les fréquences optiques des deux faisceaux F1 et F2 sont légèrement différentes. L’interférence est alors modulée temporellement, à la fréquence différence F1-F2 (typiquement quelques dizaines de MHz, voire quelques centaines) Cette modulation, appelée "battement" fournit une signature propre à l’interférence. Classiquement, la différence de fréquence est obtenue par un modulateur acousto-optique. Le schéma est alors le suivant :
Le principe de l’interférométrie hétérodyne peut être décliné de bien des façons, pour la mesure des déplacements, ou bien sûr des vitesses. Il est utilisé par exemple sur la balance du Watt, qui vise à remplacer le kilogramme étalon, pour lequel il est nécessaire de maîtriser la vitesse du fléau de la balance avec une très grande exactitude. Sur cet instrument, l’interférence hétérodyne est employée pour asservir la vitesse du fléau de la balance à être une fraction entière connue de la vitesse de la lumière.
Un peu de vocabulaire
- Détails
Il est important d’utiliser des termes qui ne soient pas équivoques. Nous évitons d’utiliser le mot "précision", car son sens n’est pas univoque. Nous utilisons deux termes, exactitude et résolution, dont le sens est bien défini (voir également la page du BIPM qui est consacrée au vocabulaire de métrologie.
L’exactitude est l’étroitesse de l’accord entre une valeur mesurée et une valeur vraie d’une grandeur à mesurer.
La résolution est la plus petite variation de la grandeur mesurée qui produit une variation perceptible de l’indication correspondante. Ainsi un instrument peut fournir une mesure très résolue mais non exacte. La résolution s’apprécie sur une durée de mesure donnée.
Les performances en exactitude et en résolution de nos télémètres vont dépendre de notre capacité à gérer les erreurs et les bruits.
L’erreur systématique est une composante de l’erreur de mesure qui, dans des mesurages répétés, demeure constante ou varie de façon prévisible.
Le bruit diffère de la notion d’erreur systématique par le fait qu’il présente un caractère aléatoire et non prévisible. C’est à priori le bruit qui va limiter la résolution de l’instrument. Mais les erreurs systématiques, si elles sont fonction de paramètres non maîtrisés, peuvent elles aussi dégrader la résolution.
Pour obtenir nos objectifs d’exactitude et de résolution, nous utilisons différentes techniques présentant des sensibilités et des intervalles de mesure différents.
La sensibilité caractérise le quotient de la variation d’une indication d’un système de mesure par la variation correspondante de la valeur de la grandeur mesurée. Si les signaux à l’entrée et à la sortie sont de même nature, la sensibilité est appelé gain.
L’intervalle de mesure est l’ensemble des valeurs de grandeurs d’une même nature qu’un instrument de mesure ou un système de mesure donné peut mesurer avec une incertitude instrumentale spécifiée, dans des conditions déterminées.
Vocabulaire encore...
Nous utilisons le terme de "télémétrie" pour désigner la mesure de la distance (absolue). Mais le même terme est parfois aussi utilisé pour désigner les instruments qui mesurent, non pas la distance, mais seulement ses variations c’est à dire les déplacements de la cible.
Les objectifs de l’activité Télémétrie Laser
- Détails
L’activité "télémétrie laser" a pour objet la mise au point de nouvelles méthodes et de nouveaux instruments permettant de mesurer des distances kilométriques avec une très haute exactitude. Quelques exemples de situations où ce type de besoins se présente :
> dans le domaine du spatial, notamment pour les missions de plusieurs satellites en vol en formation, où il est essentiel de mesurer la distance entre deux satellites avec une très grande exactitude, par exemple pour les télescopes à synthèse d’ouverture et la gravimétrie spatiale (voir le fichier "vols_en_formation.doc" ci-dessous). Carlina est un projet de télescope à synthèse d’ouverture en cours à l’Observatoire de Haute Provence.
> le positionnement de haute précision, sur terre : génie civil, grandes installations.
Les collisionneurs de particules sont des machines de dimensions hectométriques ou kilométriques, où on provoque des collisions entre deux faisceaux de particules. Encore faut-il être sûr que les faisceaux se croisent bien... et bien sûr qu’ils se croisent à l’endroit observé par les détecteurs. Or les faisceaux de particules sont des pinceaux d’un diamètre d’un ou quelques microns, voire moins... Aligner un accélérateur requiert donc une mesure de positionnement de très haute exactitude. La réalisation des grandes antennes radioélectriques pose des problèmes analogues.
> la géophysique : Surveillance des déformations du sol ou des roches, plus généralement réalisation de grands instruments à l’usage de la géophysique.
> la physique fondamentale : La navigation des satellites autour de la terre obéit aux lois de la gravitation newtonienne... sauf si on y regarde de très près : la précision atteinte maintenant par les mesures de télémétrie par temps de vol sur les satellites en orbite basse est telle qu’il faut prendre en compte les effets relativistes. Les données exploitées sont notamment celles de l’instrument T2L2. Dans ce cas la précision atteinte sur la mesure de distance est de quelques millimètres notamment du fait de la perturbation due à la traversée de l’atmosphère.
Pour toutes ces mesures la lumière d’un laser est une sonde fiable. Elle se propage dans le vide sans atténuation, si ce n’est du fait de la divergence des faisceaux laser, mais on sait produire des faisceaux très peu divergents.
Les deux projets T2M et Iliade diffèrent en cela que T2M propose des objectifs moindres en termes de résolution et exactitude, mais aussi
- par la complexité du montage : celui de T2M est très peu sophistiqué, et plus facilement embarquable
- par des méthodes différentes, notamment pour aborder les problèmes des diaphonies optiques et de diaphonies électriques.
DOCUMENT
Artémis UMR 7250
Boulevard de l’Observatoire
CS 34229 - F 06304 NICE Cedex 4
Tél. : +33 (0)4 92 00 30 11 - Fax : +33 (0)4 92 00 30 33




